今日のTLT学習　多項式×多項式（中３数学）

問題

次の計算をしなさい｡

\((x-3y)(2x-5y)=\)
\((x+7)(x+5)-(x-3)(x+6)=\)
\((x+2)(x-5)=\)
\(2x(x-2)-(3x-1)(x+2)=\)
\((3x-1)(x+2)=\)
\(-3x^2+(2x-1)(x+2)=\)
\((x+1)(y+1)=\)
\((x+5)(x-4)-(x+1)(x-1)=\)

\((x-3y)(2x-5y)\)
\(=x×2x+x×(-5y)-3y×2x-3y×(-5y)\)
\(=2x^2-5xy-6xy+15y^2\)
\(=2x^2-11xy+15y^2\)
\((x+7)(x+5)-(x-3)(x+6)\)
\(=(x^2+5x+7x+35)-(x^2+6x-3x-18)\)
\(=(x^2+12x+35)-(x^2+3x-18)\)
\(=x^2+12x+35-x^2-3x+18\)
\(=9x+53\)
\(~いきなりでちょっと,難しかったですか｡\)
\((x+2)(x-5)\)
\(=x×x+x×(-5)+2×x+2×(-5)\)
\(=x^2-5x+2x-10\)
\(=x^2-3x-10\)
\(2x(x-2)-(3x-1)(x+2)\)
\(=2x^2-4x-(3x^2+6x-x-2)\)
\(=2x^2-4x-(3x^2+5x-2)\)
\(=2x^2-4x-3x^2-5x+2\)
\(=-x^2-9x+2\)
\((3x-1)(x+2)\)
\(=3x×x+3x×2-1×x-1×2\)
\(=3x^2+6x-x-2\)
\(=3x^2+5x-2\)
\(-3x^2+(2x-1)(x+2)\)
\(=-3x^2+(2x^2+4x-x-2)\)
\(=-3x^2+2x^2+3x-2\)
\(=-x^2+3x-2\)
\((x+1)(y+1)=xy+x+y+1\)
※展開した結果,同類項がありませんから展開したままが解答になります｡
\((x+5)(x-4)-(x+1)(x-1)\)
\(=(x^2-4x+5x-20)-(x^2-x+x-1)\)
\(=(x^2+x-20)-(x^2-1)\)
\(=x^2+x-20-x^2+1\)
\(=x-19\)
※1回でできましたか｡

\(◆ 多項式の乗法\)

\( (a+b)(c+d) の計算は下のように行います｡\)
\( このように,積の形を和の形に表すことを,｢展開する｣といいます｡\)
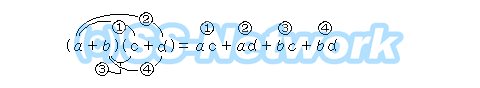
H0000280
\( 展開したあと,同類項があれば,それらをまとめます｡\)

\(（例） (x+2)(x-5)=x×x+x×(-5)+2×x+2×(-5)\)
\(~~~~~~~~~=x^2-5x+2x-10\)
\(~~~~~~~~~=x^2-3x-10\)

\( (a+b)(c+d) がなぜ ac+ad+bc+bd になるか説明します｡\)

\( c+d を 1つのかたまりと考えて E とおいてみましょう｡すると\)
\( (a+b)(c+d)=(a+b)E\)
\( =a×E+b×E \)
\( =a×(c+d)+b×(c+d) ←Eをもとに戻す\)
\( =ac+ad+bc+bd\)

当記事は、ＴＬＴソフトに収録されている問題、解説の一部を加工し掲載したものです。

上記問題が掲載されている中学３年数学TLTソフトの詳細目次はこちらでご確認いただけます。（PDF）

日米特許取得済みのＴＬＴソフトでスピード習熟しませんか？
使い放題コースなら、全100教材以上をいつでも自由に好きなだけご利用いただけます。
集中的に苦手な項目だけやるもよし。教材の使い方はあなた次第です！

まずは、無料体験をお試しください。

ＴＬＴソフトは、下記サイトでお求めいただけます。
・Newton TLTソフトウェア
・キョーイクソフトオンラインショップ